An Introduction to different Types of Convolutions in Deep Learning을 번역한 글입니다. 개인 공부를 위해 번역해봤으며 이상한 부분은 언제든 알려주세요 :)

Convolution의 여러 유형에 대해 빠르게 소개하며 각각의 장점을 알려드리겠습니다. 단순화를 위해서, 이 글에선 2D Convolution에만 초점을 맞추겠습니다

Convolutions

우선 convolutional layer을 정의하기 위한 몇개의 파라미터를 알아야 합니다

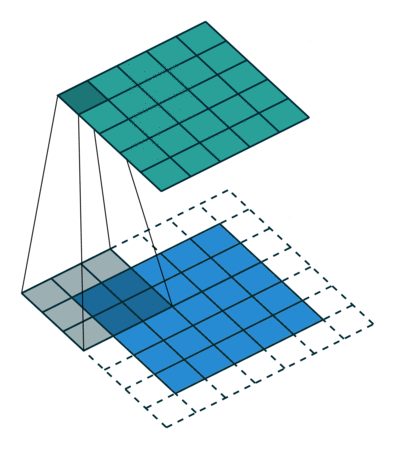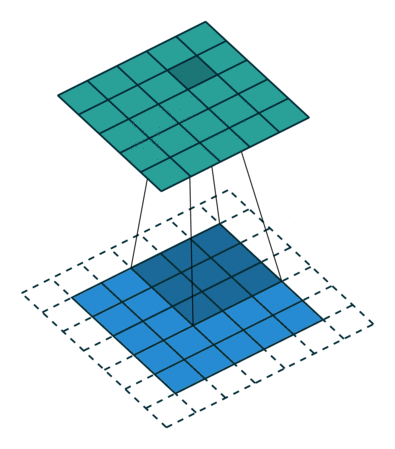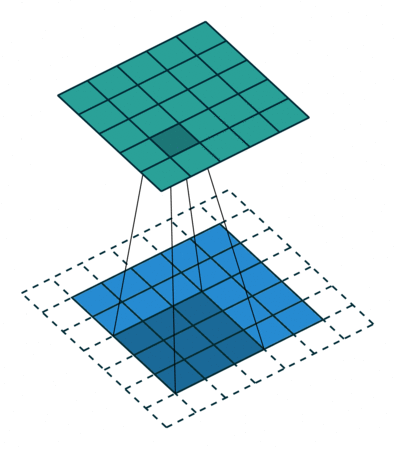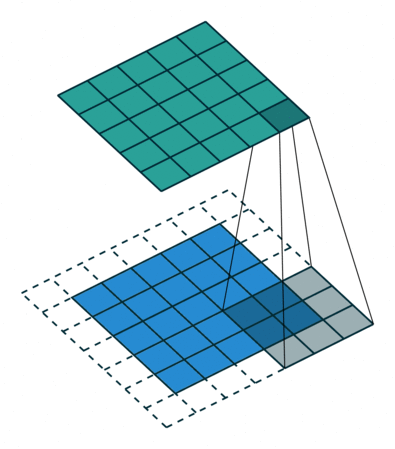
2D convolution using a kernel size of 3, stride of 1 and padding

역자 : 파란색이 input이며 초록색이 output입니다

• Kernel Size : kernel size는 convolution의 시야(view)를 결정합니다. 보통 2D에서 3x3 pixel로 사용합니다
• Stride : stride는 이미지를 횡단할 때 커널의 스텝 사이즈를 결정합니다. 기본값은 1이지만 보통 Max Pooling과 비슷하게 이미지를 다운샘플링하기 위해 Stride를 2로 사용할 수 있습니다
• Padding : Padding은 샘플 테두리를 어떻게 조절할지를 결정합니다. 패딩된 Convolution은 input과 동일한 output 차원을 유지하는 반면, 패딩되지 않은 Convolution은 커널이 1보다 큰 경우 테두리의 일부를 잘라버릴 수 있습니다
• Input & Output Channels : Convolution layer는 Input 채널의 특정 수(I)를 받아 output 채널의 특정 수(O)로 계산합니다. 이런 계층에서 필요한 파라미터의 수는 I*O*K로 계산할 수 있습니다. K는 커널의 수입니다

Dilated Convolutions ( 확장된 Convolution )

(a.k.a. atrous convolutions)

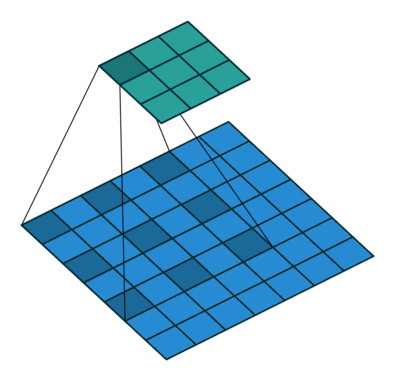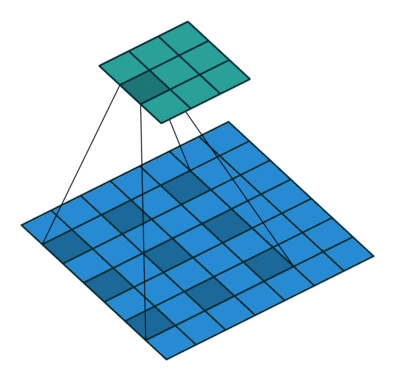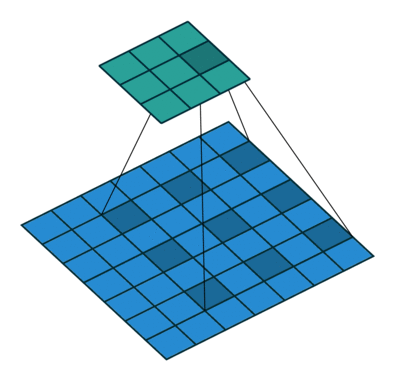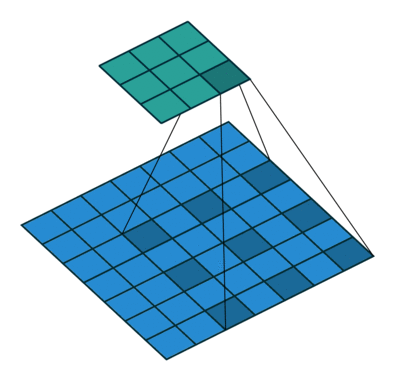
2D convolution using a 3 kernel with a dilation rate of 2 and no padding

Dilated Convolution은 Convolutional layer에 또 다른 파라미터인 dilation rate를 도입했습니다. dilation rate은 커널 사이의 간격을 정의합니다. dilation rate가 2인 3x3 커널은 9개의 파라미터를 사용하면서 5x5 커널과 동일한 시야(view)를 가집니다.

5x5 커널을 사용하고 두번째 열과 행을 모두 삭제하면 (3x3 커널을 사용한 경우 대비)동일한 계산 비용으로 더 넓은 시야를 제공합니다.
Dilated convolution은 특히 real-time segmentation 분야에서 주로 사용됩니다. 넓은 시야가 필요하고 여러 convolution이나 큰 커널을 사용할 여유가 없는 경우 사용합니다

역자 : Dilated Convolution은 필터 내부에 zero padding을 추가해 강제로 receptive field를 늘리는 방법입니다. 위 그림에서 진한 파란 부분만 weight가 있고 나머지 부분은 0으로 채워집니다. (receptive field : 필터가 한번 보는 영역으로 사진의 feature를 추출하기 위해선 receptive field가 높을수록 좋습니다)
pooling을 수행하지 않고도 receptive field를 크게 가져갈 수 있기 때문에 spatial dimension 손실이 적고 대부분의 weight가 0이기 때문에 연산의 효율이 좋습니다. 공간적 특징을 유지하기 때문에 Segmentation에서 많이 사용합니다

Transposed Convolutions

(a.k.a. deconvolutions or fractionally strided convolutions)

어떤 곳에선 deconvolution이라는 이름을 사용하지만 실제론 deconvolution이 아니기 때문에 부적절합니다. 상황을 악화시키기 위해 deconvolution이 존재하지만, 딥러닝 분야에선 흔하지 않습니다. 실제 deconvolution은 convolution의 과정을 되돌립니다. 하나의 convolutional layer에 이미지를 입력한다고 상상해보겠습니다. 이제 출력물을 가져와 블랙 박스에 넣으면 원본 이미지가 다시 나타납니다. 이럴 경우 블랙박스가 deconvolution을 수행한다고 할 수 있습니다. 이 deconvolution이 convolutional layer가 수행하는 것의 수학적 역 연산입니다.

역자 : 왜 deconvolution이 아닌지는 링크에 나와있습니다

Transposed Convolution은 deconvolutional layer와 동일한 공간 해상도를 생성하기 점은 유사하지만 실제 수행되는 수학 연산은 다릅니다. Transposed Convolutional layer는 정기적인 convolution을 수행하며 공간의 변화를 되돌립니다.

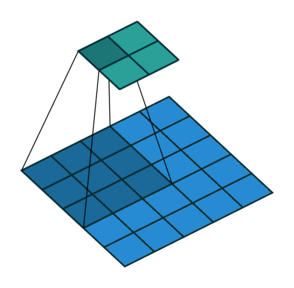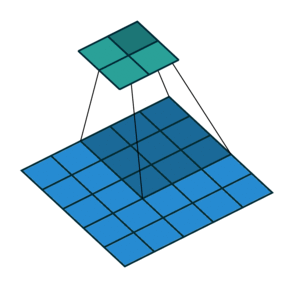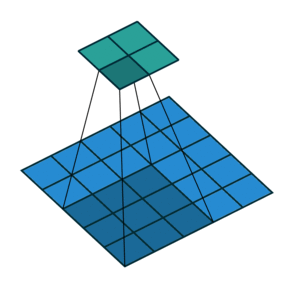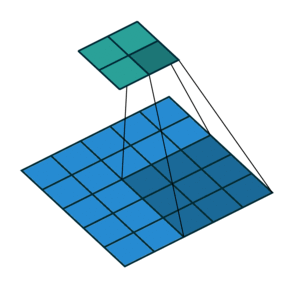
2D convolution with no padding, stride of 2 and kernel of 3

혼란스러울 수 있으므로 구체적인 예를 보겠습니다. convolution layer에 넣을 5x5 이미지가 있습니다. stride는 2, padding은 없고 kernel은 3x3입니다. 이 결과는 2x2 이미지가 생성됩니다.

이 과정을 되돌리고 싶다면, 역 수학 연산을 위해 input의 각 픽셀으로부터 9개의 값을 뽑아야 합니다. 그 후에 우리는 stride가 2인 출력 이미지를 지나갑니다. 이 방법이 deconvolution입니다

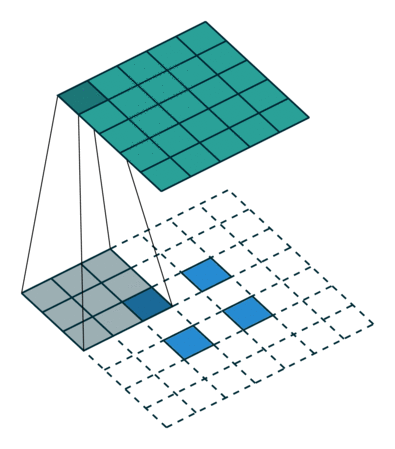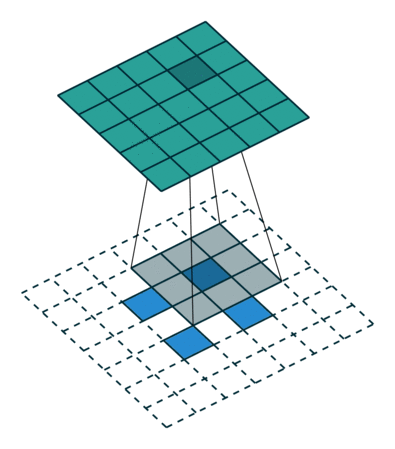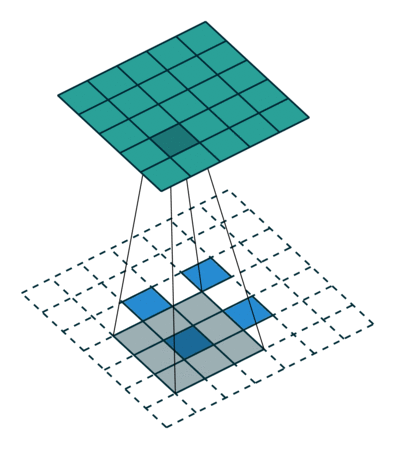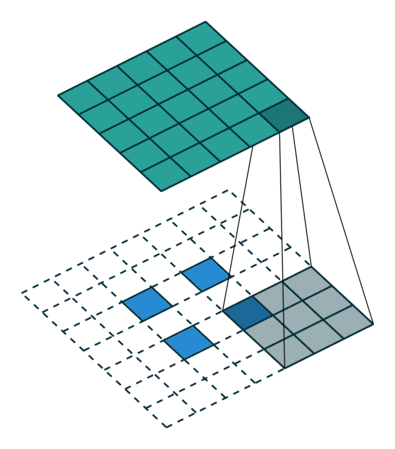
Transposed 2D convolution with no padding, stride of 2 and kernel of 3

transposed convolution은 위와 같은 방법을 사용하지 않습니다. deconvolution과 공통점은 convolution 작업을 하면서 5x5 이미지의 output을 생성하는 것입니다. 이 작업을 하기 위해 input에 임의의 padding을 넣어야 합니다.

상상할 수 있듯, 이 단계에선 위의 과정을 반대로 수행하지 않습니다.

단순히 이전 공간 해상도를 재구성하고 convolution을 수행합니다. 수학적 역 관계는 아니지만 인코더-디코더 아키텍쳐의 경우 유용합니다. 이 방법은 2개의 별도 프로세스를 진행하는 것 대신 convolution된 이미지의 upscaling을 결합할 수 있습니다

역자 : Transposed Convolution는 일반적인 convolution을 반대로 수행하고 싶은 경우에 사용하며, 커널 사이에 0을 추가합니다
위 그림은 일반적인 convolution 연산을 행렬로 표현한 것입니다

transposed convolution 연산을 행렬로 표현한 것입니다. 첫 이미지의 sparse 매트릭스 C를 inverse해서 우변(Y output)에 곱해줍니다. 그러면 Input의 값을 구할 수 있습니다.
정리하면 전치(transpose)하여 우변에 곱해주기 때문에 transposed convolution이라 부릅니다.
Up-sampling with Transposed Convolution 번역 글을 참고하시면 명쾌하게 이해가 될거에요! Convolution Operation은 input values와 output values 사이에 공간 연결성을 가지고 있습니다. 3x3 kernel을 사용한다면, 9개의 values가(kernel) 1개의 value(output, 문지른 후의 결과물)와 연결됩니다. 따라서 many to one 관계라고 볼 수 있습니다
Transposed Convolution은 1개의 value를 9개의 values로 변경합니다. 이것은 one to many 관계라고 볼 수 있습니다.
(2019년 9월) 역자 : 위 convolution 매트릭스 연산의 그림에 오류가 있습니다. 한번 어떤 부분이 오류인지 생각해보신 후, 답이 궁금하시면 댓글을 확인해주세요 :) 제보해주신 정종원님, 김남욱님 감사합니다

Separable Convolutions

separable convolution에선 커널 작업을 여러 단계로 나눌 수 있습니다. convolution을 y = conv(x, k)로 표현해봅시다. x는 입력 이미지, y는 출력 이미지, k는 커널입니다. 그리고 k=k1.dot(k2)로 계산된다고 가정해보겠습니다. 이것은 K와 2D convolution을 수행하는 대신 k1와 k2로 1D convolution하는 것과 동일한 결과를 가져오기 때문에 separable convolution이 됩니다.

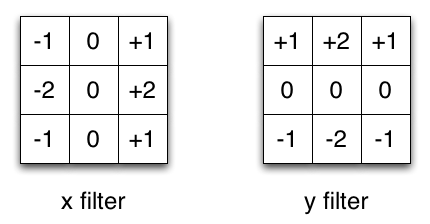
Sobel X and Y filters

이미지 처리에서 자주 사용되는 Sobel 커널을 예로 들겠습니다. 벡터 [1, 0, -1]과 [1, 2, 1].T를 곱하면 동일한 커널을 얻을 수 있습니다. 동일 작업을 하기 위해 9개의 파라미터 대신 6개가 필요합니다. 이 사례는 Spatial Separable Convolution의 예시이지만, 딥러닝에선 사용되지 않습니다

수정 : 사실 1xN, Nx1 커널 레이어를 쌓아 Separable convolution과 유사한 것을 만들 수 있습니다. 이것은 최근 유망한 결과를 보여준 EffNet라는 아키텍쳐에서 사용되었습니다.

뉴럴넷에선 depthwise separable convolution라는 것을 주로 사용합니다. 이 방법은 채널을 분리하지 않고 spatial convolution을 수행한 다음 depthwise convolution을 수행합니다. 예를 들어보겠습니다.

16개의 input 채널과 32개의 output 채널에 3x3 convolutional 레이어가 있다고 가정하겠습니다. 16개의 채널마다 32개의 3x3 커널이 지나가며 512(16*32)개의 feature map이 생성됩니다. 그 다음, 모든 입력 채널에서 1개의 feature map을 병합하여 추가합니다. 32번 반복하면 32개의 output 채널을 얻을 수 있습니다.

같은 예제에서 depthwise separable convolution을 위해 1개의 3x3 커널로 16 채널을 탐색해 16개의 feature map을 생성합니다. 합치기 전에 32개의 1x1 convolution으로 16개의 featuremap을 지나갑니다. 결과적으로 위에선 4068(16*32*3*3) 매개 변수를 얻는 반면 656(16*3*3 + 16*32*1*1) 매개변수를 얻습니다

이 예는 depthwise separable convolution(depth multiplier가 1이라고 불리는)것을 구체적으로 구현한 것입니다. 이런 layer에서 가장 일반적인 형태입니다.

우리는 spatial하고 depthwise한 정보를 나눌 수 있다는 가정하에 이 작업을 합니다. Xception 모델의 성능을 보면 이 이론이 효과가 있는 것으로 보입니다. depthwise seprable convolution은 매개변수를 효율적으로 사용하기 때문에 모바일 장치에도 사용됩니다

역자 : 채널, 공간상 상관성 분리를 하는 인셉션 모델을 극단적으로 밀어붙여 depthwise separable convolution 구조를 만듭니다. input의 1x1 convolution을 씌운 후 나오는 모든 채널에 3x3 convolution을 수행합니다. 원글에서 separable convolution의 설명이 부족한 것 같아 PR12의 영상을 보고 이해했습니다
유재준님의 PR-034: Inception and Xception과 이진원님의 PR-044: MobileNet을 보면 이해가 잘됩니다 :)

Questions?

이것으로 여러 종류의 convolution 여행을 끝내겠습니다. Convolution에 대한 짧은 요약을 가지고가길 바라며 남아있는 질문은 댓글을 남겨주시고, 더 많은 convolution 애니메이션이 있는 Github를 확인해주세요

번역시 참고한 자료

• 라온피플 Deconvolutional Network
• 라온 피플 Dilated Convolution
• 라온 피플 Semantic Segmentation
• Separable Kernel Convolution
• MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
• Convolution Arithmetic in Deep Learning Part 2
• Tensorflow KR - PR12 유튜브 강의

카일스쿨 유튜브 채널을 만들었습니다. 데이터 사이언스, 성장, 리더십, BigQuery 등을 이야기할 예정이니, 관심 있으시면 구독 부탁드립니다 :)

PM을 위한 데이터 리터러시 강의를 만들었습니다. 문제 정의, 지표, 실험 설계, 문화 만들기, 로그 설계, 회고 등을 담은 강의입니다

이 글이 도움이 되셨거나 다양한 의견이 있다면 댓글 부탁드립니다 :)